黄金比と数列
造形の秩序を支える美的形式原理である黄金比と数列の基本を学びましょう。
黄金比とは
黄金比はAとBとの割合がA:B=B:(A+B)の関係をいいます。
その比率はA:B=1:1.618です。
黄金比は古代エジプト時代に考案されたと考えられています。クフ王のピラミッドの底辺と高さの比率も黄金比になっています。
その後、古代ギリシャ人によって、彫刻、神殿などに取り入れられています。特に人体の肉体美の美意識をもって黄金比が取り入れられたことが特徴的といえます。
ルネッサンス期にはキリスト教の建造物や美術の多くに黄金比が採用されて、ものの美しさの尺度(モデュール)として黄金比が神聖化されて定着します。
現代ではデザイン、建築、美術など分野を問わずその黄金比の美しさが取り入れ、見た目だけでなく機能美に関しても注目されています。
0.618
|
1
|
1.618
|
2.618
|
さまざまな数列
■等差数列…同じ差を保ちながら変化していく数列。
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
■等比数列…同じ比率を保ちながら変化していく数列。
1 |
2 |
4 |
8 |
16 |
32 |
■フィボナッチ数列…0,1,1,2,3,5,8,13,21,34,55,89,144,…と変化していく数列です。このフィボナッチ数列の特徴は、黄金比へ近づいているところです。55:89は、1:1.6181818...という比率です。フィボナッチ数列はひまわりの種の配列や巻貝など動植物に準拠していることが発見され、改めて黄金比の素晴らしさ、美しさが確信的になりました。
| 0 |
1 |
1 |
2 |
3 |
5 |
8 |
13 |
21 |
■調和数列…数列の各項の逆数を各項とする数列が等差数列となるとき、もとの数列を調和数列という。
1/1 |
1/2 |
1/3 |
1/4 |
1/5 |
1/6 |
1/7 |
1/8
|
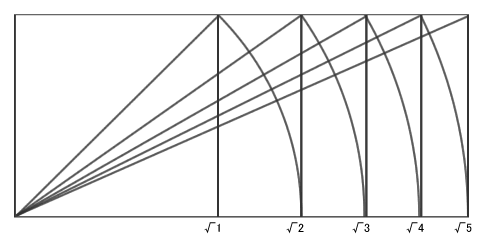
■ルート矩形…ルート矩形は実用的な形で私達は日常なじみがある比率といえます。
例えば1:√2ですと官製ハガキ、洋形封筒2号、用紙サイズA版・B版、新聞全段などで使用されています。その比率は半分に折りたたんでいっても変化することはなく実用的といえます。
1:√4ですと日本の文化では生活の中で多く活用され、畳や襖、屏風などで使用されます。
1:√5では、新聞広告全5段、洋形封筒4・5号、長形封筒2・4号などで使用されます。