群化
『群化』は絵画上にある形や色のまとまり方を知覚する法則です。
群化による知覚の法則や心理作用を理解すれば、鑑賞者の視線を誘導することができるので、デッサンや絵画制作で大いに役立ちます。
ここでは主に9つの要因に分けて、まとまりを知覚する要因について考えていきたいと思います。
このページの目次
絵画における群化の法則[YouTube動画]
絵画上にある形や色をまとまりとして知覚する群化の法則ついて解説している動画です。
ページの内容と共に参考にしてください。ぜひチャンネル登録お願いします。
群化の法則-まとまりを知覚する9つの要因
近接の要因による群化
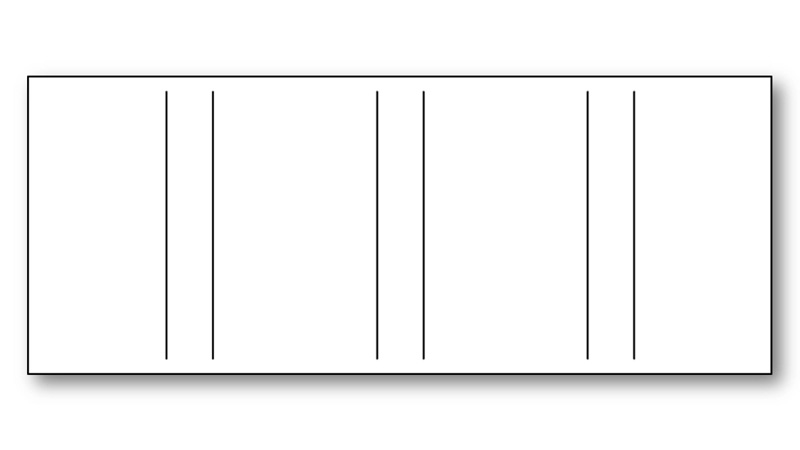
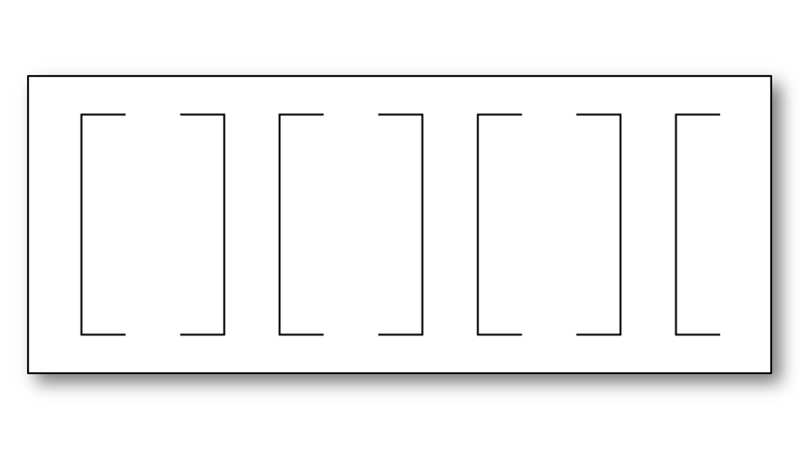
上の図には6本の線が縦に描かれていますが、どのようなまとまりとして知覚されるか感じてみてください。
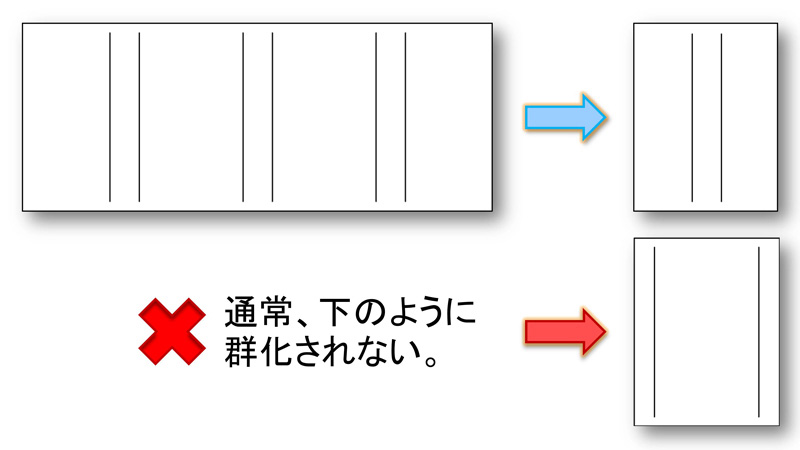
一般的には近接にある線同士が一組として知覚されやすいので、この図では近接な2本の線を一組とした3組がまとまりをもって図として知覚されます。
赤い矢印で示したように、離れた線同士を一組のまとまりとして見ることは通常ありません。
これが『近接の要因による群化』です。
人によっては離れた線同士を一組の図として認識する人もいるでしょうし、階段の段のような認識をする人もいるでしょうが少数派と考えられています。
類同の要因による群化・ケース1
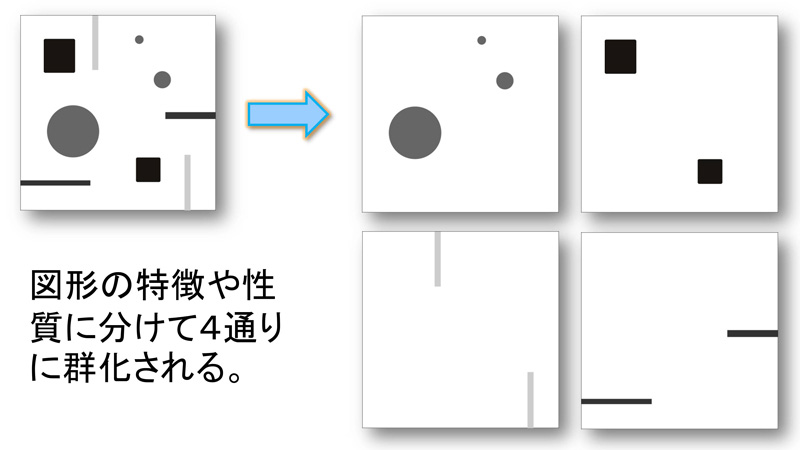
上の図の『類同の要因による群化』では、似たような特徴を持った形や線などが距離に関係なくまとまります。
このように、矢印で示した4通りの図形にまとまって知覚されると思います。
正方形や正円は、同じ図形でまとまり、大きさの変化が奥行きを感じさせます。
同じ形状の長方形は、明度の差でまとめられています。
類同の要因による群化・ケース2
この図からも『類同の要因による群化』を知覚してみてください。
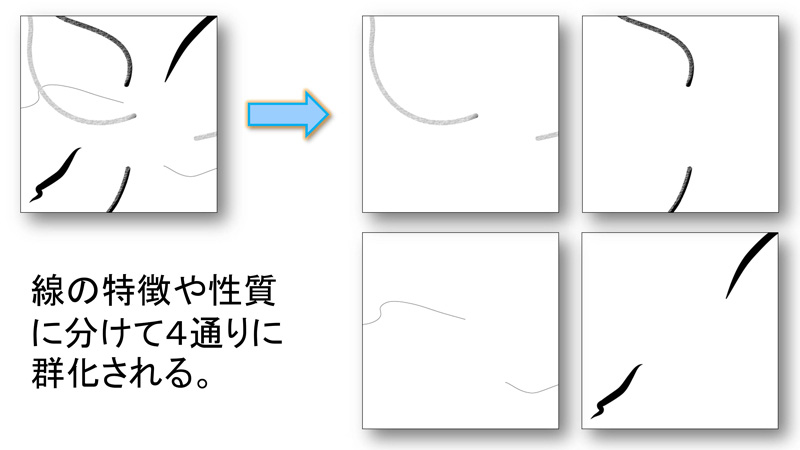
この図では、線の特徴から、まとまりを知覚できると思います。 これも距離に関係なく認識されます。
線の特徴で分けると、矢印で記した4通りの線としてまとまって知覚されると思います。
線も図形の場合と同じように、特徴の違いで分類されて、まとまることが分かると思います。
デッサンの時によくニュアンスをかえて描こうとする時、この類同の要因をうまく利用して描くことができれば、表現力が増します。
類同の要因では、同じ性質同士がまとまりやすいと考えられますが、形よりも色の性質のほうがまとまりやすい傾向があります。
閉合の要因による群化
『閉合の要因による群化』では、閉じた領域、あるいは閉じた領域をつくろうとするもの同士がまとまります。
閉じられる線であることを認識できるかどうかが閉合の要因として重要です。
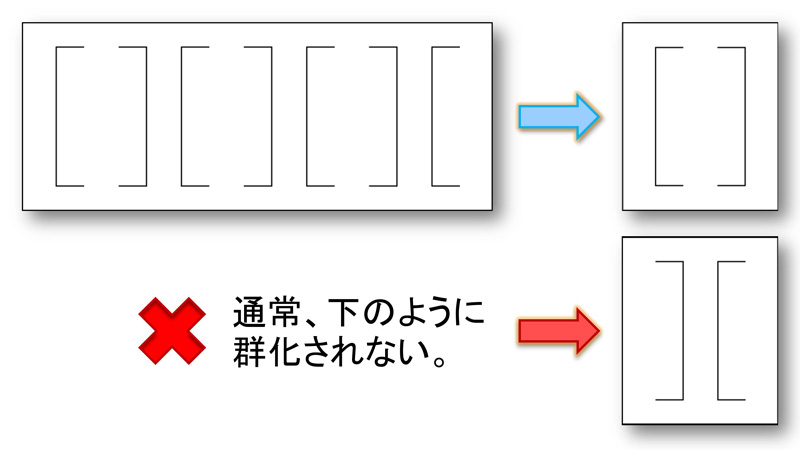
文章で使用されるカギかっこがまとまって見えるのはこの要因によります。すでにお分かりだと思いますが、青い矢印で示したように閉じた領域をつくろうとする線が一組になってまとまります。
通常、赤い矢印で示したようにまとまって見えることはありません。
もし形が向かい合わずに同じ方向を向いていれば類同の要因によって、すべてが群化されると考えられます。
良い連続の要因による群化
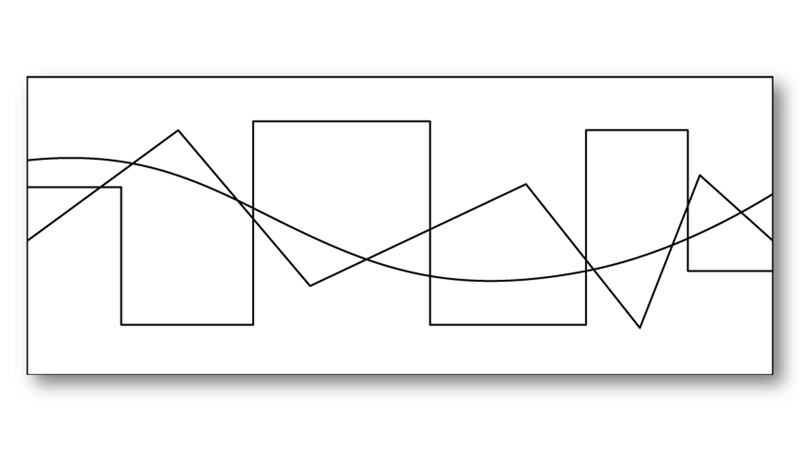
この図には直線や曲線が入り乱れていますが、基本的には特性のある3つの線でできています。
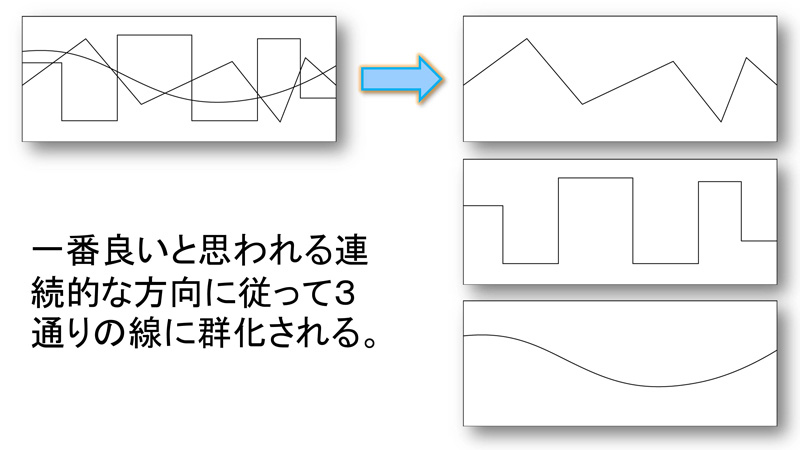
『良い連続の要因による群化』では、一番良いと思われる連続性を一つのまとまりとして知覚します。
この青い矢印で示したように、3通りの線に分けてまとめることができると思います。
共通運命の要因による群化
『共通運命の要因による群化』では、同じように動くものは距離に関係なく一つにまとまります。
このとき、近接の要因や類同の要因よりも強くまとまるので、同じ動きをする図形は、異なる形状や色彩でも群化します。
それを理解するために図には2つの色彩を配色し、2つの図形を採用してランダムに配置しています。
図形が同じ動きをしている間は、すべてが一つにまとまります。その後、違う動きを示したときから、それぞれの動き方をする図形同士でまとまります。
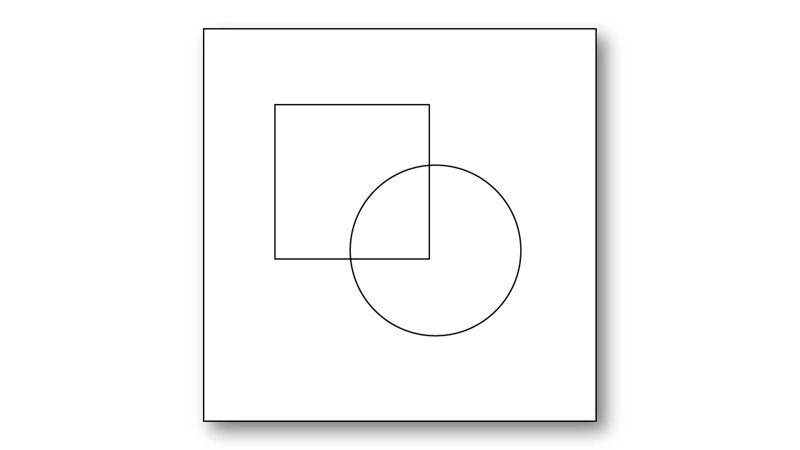
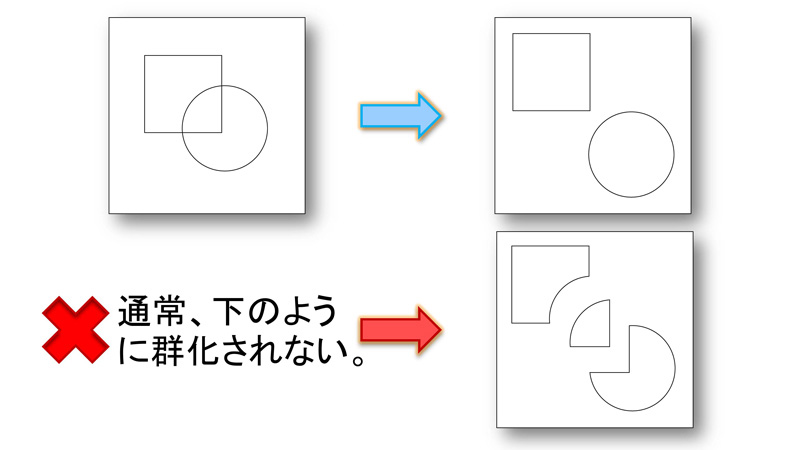
良い形の要因による群化
『良い形の要因による群化』では、規則的、対称的、完結、単純な方向に向かって図形がまとまります。
この図形では、青い矢印で示したように、対称的で単純な正四角形と正円でまとまります。
赤い矢印で示したように図形が複雑に細かく分かれてまとまることはありません。
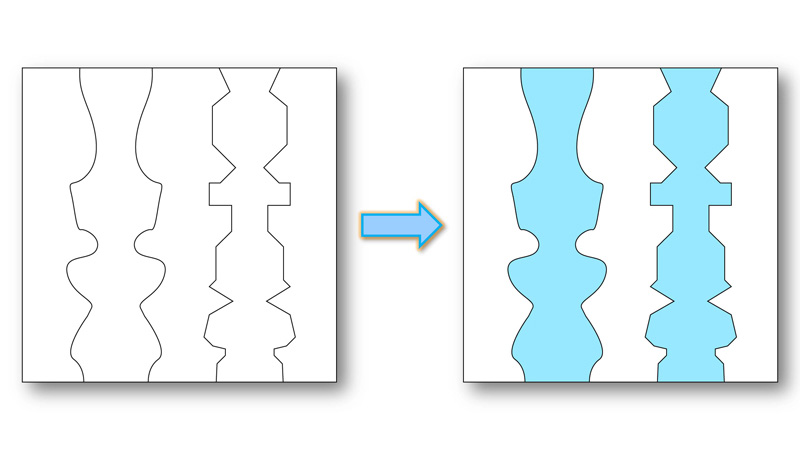
対称性の要因による群化
『対称性の要因による群化』では、対称の形をした図形がまとまって知覚されます。
この図形の場合、水色で示した形が図となり、まとまります。
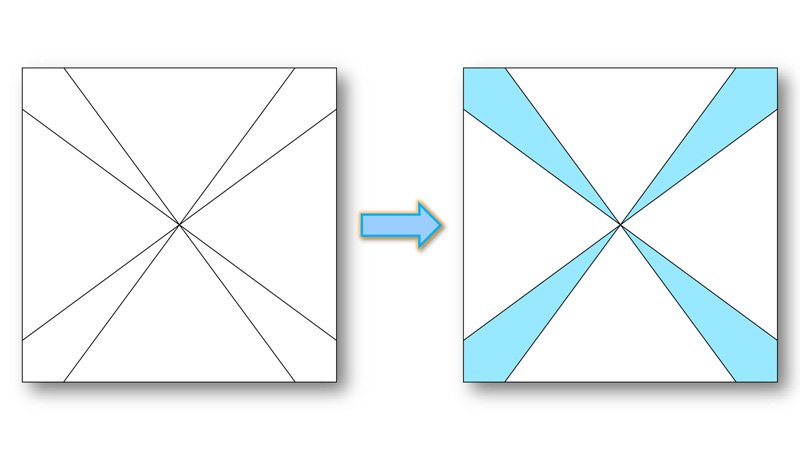
面積の要因による群化
『面積の要因による群化』では、図形の中にある面積比の小さい形が図となり、まとまりを感じられます。
この図形では、水色で示した形が図となり、まとまります。
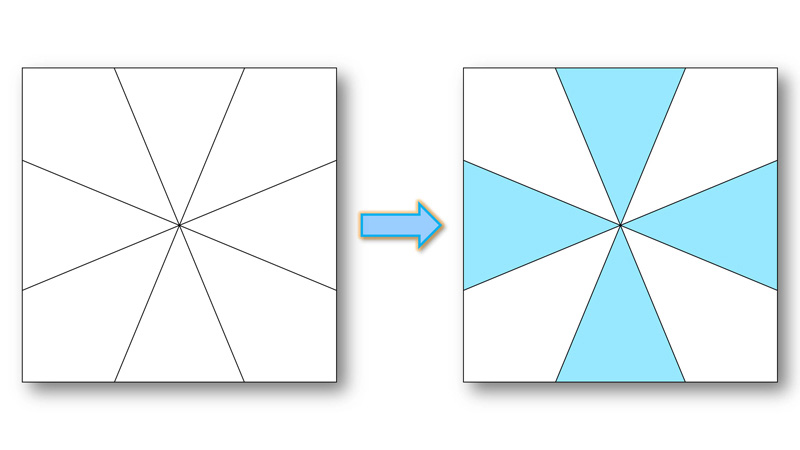
方向の要因による群化
『方向の要因による群化』では、水平と垂直方向にある形が図となり、まとまりを感じられます。
この図形では、水色で示した形が図となり、まとまります。
以上が『群化の法則』の9つの要因になります。
最後は群化の法則の要因のまとめです。
おさらいしましょう。
群化の法則(まとめ)
- 『近接の要因』では、近くにあるもの同士がまとまる。
- 『類同の要因』では、同じような特徴を持ったもの同士が、距離が離れていてもまとまる。
- 『閉合の要因』では、閉じられようとするもの同士がまとまる。
- 『良い連続の要因』では、点や線が一番良いと思われる連続的な方向に従って一つにまとまる。
- 『共通運命の要因』では、同じように動くものは距離に関係なく一つにまとまる。
- 『良い形の要因』では、規則的、対称的、完結、単純な方向に向かって図形がまとまる。
- 『対称性の要因』では、対称の形が図となり、まとまる。
- 『面積の要因』では、図形の中にある面積比の小さい形が図となり、まとまる。
- 『方向の要因』では、水平と垂直方向にある形が図となり、まとまる。
今回、多くの群化の法則の要因にふれてきましたが、実際の絵画は、これらの要因が複雑に絡み合っています。
そのことを踏まえて、群化の法則をうまく使いこなしてほしいと思います。